Topological pair

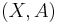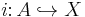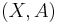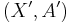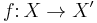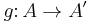In mathematics, more specifically algebraic topology, a pair $(X,A)$ is short-hand for an inclusion of topological spaces $i\colon A\hookrightarrow X$ . Sometimes $i$ is assumed to be a cofibration. A morphism from $(X,A)$ to $(X',A')$ is given by two maps $f\colon X\rightarrow X'$ and $g\colon A\rightarrow A'$ such that $i' \circ g =f \circ i$ .

Pairs come up mainly in homology theory and cohomology theory, where chains in $A$ are made equivalent to 0, when considered as chains in $X$ .

Heuristically, one often thinks of a pair 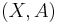$(X,A)$ as being akin to the quotient space $X/A$ .

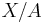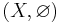There is a functor from spaces to pairs, which sends a space $X$ to the pair $(X,\varnothing)$ .

Topological pair

References